ピタゴラス勝率(ピタゴリアン期待値)
ピタゴラス勝率(ピタゴリアン期待値)に関係する数式等
勝つこととは、相手より多く得点すること
野球に限らず得点を競うスポーツは、当然ながら得点の多い方の勝ち。要するに下のような式で表すことができます。
- チームの得点>チームの失点=勝利
- チームの得点<チームの失点=敗戦
- チームの得点=チームの失点=引分
野球でいうと「投手が自軍の得点より少ない失点に抑え、打線が投手の失点より多く得点すること」が勝利の条件。
そうなると、チームが勝つためには「得点を増やして失点を減らす」という編成が必要になり、その手段として「補強」があります。主に以下のような選手の獲得に動きます。
- 防御率の良い投手や、勝利数・ホールド数・セーブ数の多い投手。
- 打率・打点の高い打者。
- 守備・走塁に長けた選手。
しかし、弱点の補強だけで勝てるかというと、チーム編成はそう簡単ではありません。
「チームは”選手”を買うのではなく、”勝利”を買うべきだ」という格言は、映画「マネーボール」で登場します。バスケ漫画の「あきらめたら、そこで試合終了だよ」と同じくらいの名言といっても過言ではありません。
「勝利を買う」ということは、正に「相手より多く得点するチームを作る」ということです。しかし過去のプロ野球を見ても分かるとおり、なりふり構わず補強したからといって、必ずしも強いチームには仕上がりません。どうすれば強くなるか、しっかりした目的の下で補強する必要があります。
そこで、勝つためにはどのような選手が必要かを見るための指標のひとつに「ピタゴラス勝率」があります。チームが、得点を増やすのが先か、失点を防ぐことが先かということを導き出すことができます。
得点と失点の差から、勝率を予測する「ピタゴラス勝率(ピタゴリアン期待値)」
チームを編成する指標のひとつに「ピタゴラス勝率(ピタゴリアン期待値)」というものがあります。中学で習う三角形の計算「ピタゴラスの定理(三平方の定理)」が名前の由来となりました。
ピタゴラス勝率は「得点と失点の差で、どれだけの勝率が見込めるか?」という指標です。
この指標を使い「どれだけ得点数を増やし」て「どれだけ失点を減らす」と「おおよそ何勝できるか」を予測します。
ピタゴラス勝率(ピタゴリアン期待値)の求め方
ピタゴラス勝率の計算方法は以下のとおり。

この式から、得点と失点の差で、おおよその勝率を予測します。特徴としては以下のようになります。
- 得点と失点が同じ場合、ピタゴラス勝率は5割になる
- 得点が失点を上回れば勝率は5割を超え、その反対は5割に満たない
計算式の指数は、得点と失点の2乗になっていますが、指数はリーグによって補正されます。例えば、NPBでは2乗ではなく「1.6乗~1.7乗」となり、年代によっても変化します。指数については膨大なデータを使って算出しますので、割愛します。
実際の勝率と得失点差の因果関係は?
ピタゴラス勝率は、単純に得失点差がプラスになる程高くなり、マイナスになる程低くなります。
下の図-1グラフは、2012年~2021年のプロ野球順位の分布です。12球団の勝率と、得失点差の関係を示したものです。中央の赤い線に集中するほど、ピタゴラス勝率に近いということになります。ほぼ、中央の線に集まっているところから、ピタゴラス勝率はおおよその予測どおりになるということが分かります。
しかし、ピタゴラス勝率は「指標」のひとつに過ぎません。指標とは、必ずそうなるというものではないので、大きく離れる場合もあります。それを証明するかのような成績もあります。下のグラフ内の吹き出しの位置は、実際の勝率と得失点差が大きく離れた結果を指しています。
図-1
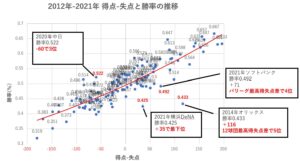

実は名将だった与田監督
2020年の中日は、得失点差が‐60でした。失点が得点を大きく上回りましたが、勝率は5割を超えAクラスとなったのです。反対に、2014年のオリックスは得失点差116で12球団最高だったにもかかわらず、実際の勝率が5割に満たず、順位も5位となっています。「野球の勝敗は、戦力だけでは決まらない」という証明といえるでしょう。
この表から2020年の中日は、「与田監督の采配がすばらしかったチーム」ということが見えてきます。
戦力が乏しいチームを応援しているのに、なぜか野球から目が離せないという心理は、その辺にあるのかも知れません。
ピタゴラス勝率の名前の由来 ピタゴラスの定理
「ピタゴラス勝率」という名前の由来となった「ピタゴラスの定理」。中学時代は「社会に出たら使わない勉強」と思っておりましたが、私は機械設計業務に就いた都合で、日常的に使うことになりました。そして今、野球を楽しむために再認識することになったのですから、本当に、どこで何が役に立つのか分からないものです。


