ピタゴラスの定理
この数学が必要なセイバーメトリクスの指標
- なし。ピタゴラス勝率（ピタゴリアン期待値）と、ピタゴラスの定理には、計算式や考え方に具体的な関係はありません。単に、計算式が似ているから名付けられただけです。しかしせっかくですから、ピタゴラスの定理の証明を調べてみました。
「ピタゴラスの定理」を求めよう
直角三角形で、直角の向かいにある「斜辺c」と。直角をはさむ2つの辺a,bの関係は
次の式で成り立つ、という定理です。
c²=a²+b²
しかし言葉だけでは、何をいっているのか分からないのが正直なところ。このような公式は、単純に暗記するよりも「どうしてこの式が成り立つか？」という原理を理解することが大切です。そうすると記憶に定着しやすくなり、公式の応用がしやすくなります。（年を取るとなかなか覚えられませんが（笑））
三平方の定理を証明する方法は多々存在しますが、ここでは最もポピュラーな証明の方法で見てみましょう。
まずは図-1の三角形の斜辺cを求める式は、以下のようになります。
図-1
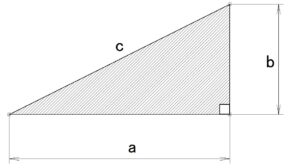
c²=a²+b²
∴c=√a+b
実際に求めてみます。図2-1のように、直角三角形に a＝50(高さ)、b＝100(底辺) の数を付与します。この値から、c(斜辺)を求めます。
図2-1
次に、図2‐1の三角形を4個、図3‐2のように並べます。そうすると1辺が150の正方形となり、中央の空白部分に1辺を c(斜辺) とする正方形が出来ます。ここの面積は「c×c」、つまり「c²」になります。
図2‐2
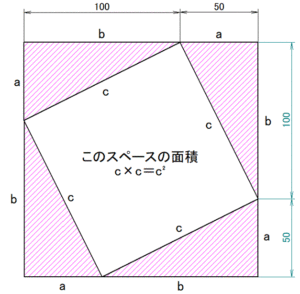
次に、外側の辺を150にしたまま、三角形の位置を変えます。ここで確認しておきたいことが1つ。1辺が150の正方形内に、同じ三角形が4個という条件は、図2‐2と同じです。ということは、形は変わっても「空白部分の面積は、図2‐2＝図2‐3」となることを押さえておきましょう。
図2‐3
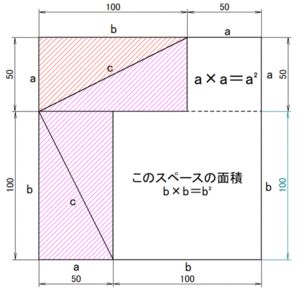
そうすると、図2‐3で空白部分の面積を求めるには、「a×a」「 b×b」となり、その合計が面積となります。
- a×a＋b×b＝空白部分の面積
- つまり「a²＋b²」
ここで、「空白部分の面積は、図2‐2＝図2‐3」という条件を持ってくると、
c²=a²+b²
∴c=√a+b
ということが証明出来ます。
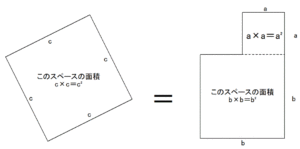
要するに、以下のような証明です。
- 同じ150×150の正方形内に、同じ直角三角形4個が入る。
- 図2‐2、図2‐3の三角形が占有している面積と、空白部分の面積は同じ。
- よってc×c=a×a＋b×b(c²=a²+b²)、c=√a+bが成り立つ。
まとめ ピタゴラス勝率とピタゴラスの定理は因果関係無し
以上のように、「ピタゴラス勝率」と「ピタゴラスの定理」をそれぞれ見てみましたが、この二つに因果関係はありません。単に「式が似ているから」その名前を付けたというだけです。
ピタゴラスの定理を振り返ってはみましたが、セイバーメトリクスには使いません（笑）。
とはいえ、近年は野球の指標で「打球の角度と速さ」が注目され始めています。既に、一部の球場ではビジョンに表示されるようになりました。今後、ピタゴラスの定理が野球を楽しむために役立つかも知れません。
振り返り学習は、きっかけが大切。もしも興味が出ましたら、得失点差と勝率を気にかけてみてください。そうして新しい角度から野球を楽しんでいただけることを、心より願っております。
